Linear Algebra I: Homework 1
-
-
Find all solutions of the system of linear equations
\[\begin{aligned} 3x + 5y &= 3 \\ 5x - 6y &= 0 \end{aligned}\]Solving the first equation for \(x\) yields,
\[x = \frac{3-5y}{3}.\]Once we plug this in for \(x\) in the second equation and solve for \(y\), we get that,
\[\begin{aligned} 5x - 6y &= 0 \\ 5\left(\frac{3-5y}{3}\right) - 6y &= 0 \\ 5(3-5y) &= 18y \\ 15 - 25y &= 18y \\ 15 &= 43y \\ \frac{15}{43} &= y \end{aligned}\]Plugging this \(y\) into our earlier equation for \(x\) gives,
\[x = \frac{3-5\left(\frac{15}{43}\right)}{3} = \frac{18}{43}\] -
On a single coordinate plane, sketch a line for each linear equation in the above system, then point out in your graph where your solution from part (a) is.
The red line is the first equation, and the blue is the second. The green marked intersection is the solution of the system.
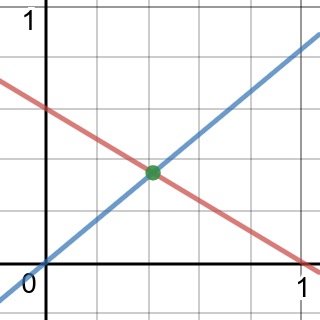
-
-
Find all solutions of the system of linear equations
\[\begin{aligned} 5x_1 + x_2 &= -3 \\ 10x_1 + 2x_2 &= -6 \end{aligned}\]The second equation is twice the first equation, and can be eliminated by an elementary row operation. So, \(x_2\) is free, and all solutions are described as
\[\left( \frac{-3-x_2}{5}, x_2 \right).\]There are other valid ways to write this solution, too.
-
Write down a system of linear equations that has no solutions.
There are many different solutions here. One example is the system,
\[\begin{aligned} x &= 0 \\ y &= 0 \\ x + y &= 1, \end{aligned}\]Describing three lines that do not have a common intersection point.
Another valid solution would be the parallel planes,
\[\begin{aligned} x + y + z &= 1 \\ x + y + z &= 2. \end{aligned}\] -
Write down an augmented matrix corresponding to the system of linear equations,
\[\begin{aligned} 4a + c - d &= 9 \\ 2b + c + d &= 3 \\ a + b + c + d &= -1 \\ 4b &= 8 \end{aligned}\]This system translates into the augmented matrix,
\[\left( \begin{array}{cccc|c} 4 & 0 & 1 & -1 & 9 \\ 0 & 2 & 1 & 1 & 3 \\ 1 & 1 & 1 & 1 & -1 \\ 0 & 4 & 0 & 0 & 8 \end{array} \right),\]Provided the columns describe (in order) the variables \(a, b, c, d\).